组合数学杨辉-高斯级数--等幂求和，显然易证故得到：

#include<bits/stdc++.h> using namespace std; int main() { long long n; cin>>n; cout<<(n*(n+1)(2n+1))/6<<endl; return 0; }

思路

很显然用 O(1) 的平方和公式：

$$\sum_{i = 1}^{n} i^2 =\frac{n(n+1)(2n+1)}{6}$$

证明如下：

code

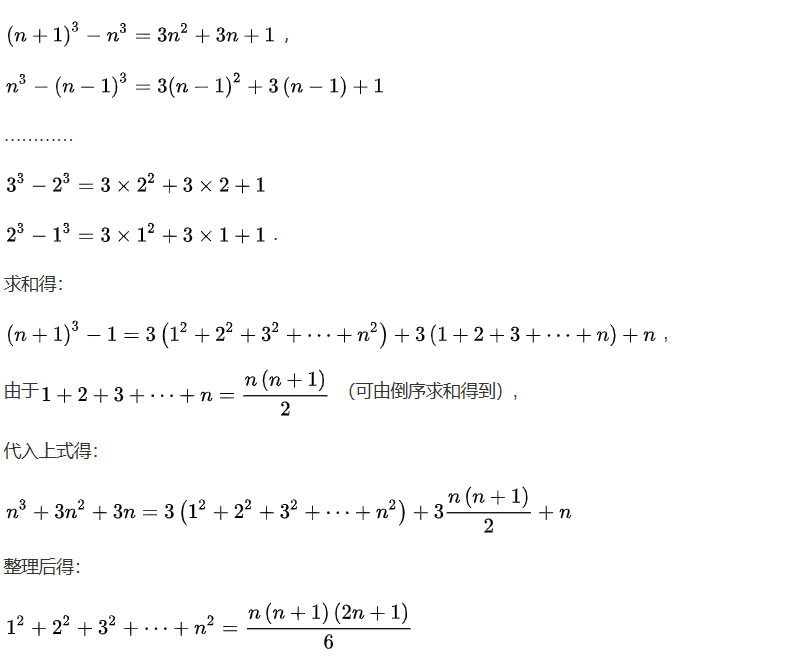
#include<bits/stdc++.h>
using namespace std;
int main(){
   int n;
   cin>>n;
   cout<<(n*(n+1)*(2*n+1)/6);
   return 0;
}

#include<bits/stdc++.h> using namespace std; int main() { int n,sum=0; cin>>n; for(int i=1;i<=n;i++) { sum=sum+i*i; } cout<<sum; return 0; }

#include<bits/stdc++.h> using namespace std; int main(){ int n,ans=0; cin>>n; for(int i=1;i<=n;i++) { ans=ans+i*i;} cout<<ans; return 0; }

#include<bits/stdc++.h> using namespace std; int main() { int n,s=0; cin>>n; for(int i=1;i<=n;i++) { s=s+i*i; } cout<<s<<endl; return 0; }

#include<bits/stdc++.h>

using namespace std;

int main()

{

int n,sum=0;

cin>>n;

for(int i=1;i<=n;i++)

{

sum=sum+i*i;

}

cout<<sum;

return 0;

}

#include<bits/stdc++.h>

using namespace std;

int main()

{

int n,sum=0;

cin>>n;

for(int i=1;i<=n;i++)

{

sum=sum+i*i;

}

cout<<sum;

return 0;

}